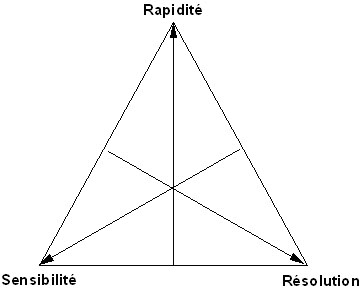
Figure 6-1 : Triangle des compromis
|
COURS
DE CHROMATOGRAPHIE
(Master de Chimie 1ère année)
Faculté des
Sciences d'Orsay
- Généralités
sur la chromatographie
- Théorie de la chromatographie 1 - Théorie de la chromatographie 2 - Théorie de la chromatographie 3 - La chromatographie en phase gazeuse (CPG) - Analyse en chromatographie en phase gazeuse - Optimisation d'une analyse - Le triangle des
compromis
- Glossaire- Optimisation des quantités à injecter - Optimisation par le facteur de séparation - Optimisation par le facteur de rétention - Optimisation par le nombre de plateaux théoriques - Optimisation par la vitesse de la phase mobile - Conclusion sur l'optimisation - Problèmes sur l'optimisation |

Figure 6-2 : Séparation de deux pics en chromatographie |
La
résolution est donnée par la formule de Purnell
(équ.3-8), où 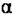 = t'rB/t'rA
et k' =k'B = t'rB/t'rA
et k' =k'B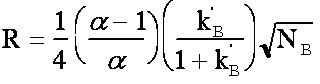 (equ.
3-8) (equ.
3-8) |
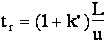 (eq. 6-1)
(eq. 6-1)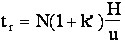 avec la formule de Purnell
tr
se présente comme
suit :
avec la formule de Purnell
tr
se présente comme
suit : 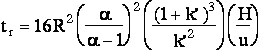 (eq.6-2)
(eq.6-2)l'expression (6-2) est approchée, car H est fonction de u, mais si u>>uopt l'équation de Van Deemter montre que (H/u) est à peu près constant.
Les expressions (3-8) et (6-2) dépendent donc du même jeu de 3 paramètres a, k' et N. Pour conduire l'optimisation on fera varier chaque paramètre6-2 OPTIMISATION DES QUANTITES A INJECTER
La quantité de soluté qui peut être injectée dans une colonne varie avec les différents types de chromatographie. On peut définir deux termes Q0 et Qs:
Q0
est la quantité minimum détectable (pour avoir un
rapport
signal sur bruit S/N=4). Ce paramètre dépend
essentiellement de la sensibilité du détecteur du
chromatographe.
6-3-OPTIMISATION PAR LE FACTEUR DE SÉPARATION (a)
Si
on augmente le facteur de séparation (la
sélectivité) a,
c'est
à dire la différence
d'énergie libre de dissolution dr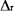 G)
entre
les deux produits, la résolution augmente d'après
l’équ.3-8).
G)
entre
les deux produits, la résolution augmente d'après
l’équ.3-8).
a=(tr(B)-tm)/(tr(A)-tm) est toujours supérieur à 1.
En théorie, comme le montre la courbe ci-dessous, de faibles variations de a au voisinage de 1 peuvent entraîner de grandes variation de la résolution.
|
Figure
6-3 Variation de la résolution en fonction de a.
|
Figure
6-4 Influence de a
sur la Résolution de 2 pics (k' et N sont invariants)
|
La
résolution double (entre 0,1 et 0,2) si a
varie entre
1,11 et 1,25., donc
augmente de 14% seulement.
En
pratique, il faut toujours prendre le bon
couple (phase
mobile/phase stationnaire) pour que le paramètre a
soit >
1,5
et
permette ainsi une séparation facile.
Solution.
| a | 1,25 |
1,20 |
1,10 |
1,05 |
| R | 1,5 |
1,25 |
0,68 |
0,36 |
| Le
temps d'analyse est extrêmement sensible au
paramètre a
si il
est inférieur à 1,5, il
augmente énormément si a
diminue.
Les
diminutions du facteur de
séparation se payent donc cher en temps
d'analyse lorsque a
est trop
petit. En
revanche lorsque a
est
supérieur à 2 le temps d''analyse est
relativement
insensible à ce terme. |
Figure 6-5 Variation du temps d'analyse en fonction de 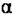 . . |
|
Pratiquement. Lorsque a est proche de l'unité, cela signifie que la différence d'énergie libre de dissolution entre les 2 produits est trop faible, il faut donc augmenter a. On peut: 1- soit changer la composition de la phase mobile en HPLC (impossible en CPG)2- soit prendre une phase stationnaire différente, ce qui revient à alors changer de colonne. 3- en CPG, diminuer la température, car lna = -( 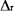 G°(B)
- G°(B)
- 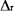 G°(A))/
RT G°(A))/
RT |
6-4-OPTIMISATION PAR LE FACTEUR DE RÉTENTION (k')
|
Figure
6-6 Variation de la résolution en fonction de k'.
|
Figure
6-7 Influence de k'
sur la Résolution de 2 pics (
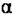 et N sont invariants)
et N sont invariants) |
6-4-2- Influence sur le temps d'analyse
D'après l’équ.6-2, le terme y=(1+k')3/k'2 est minimum pour k'=2 puis il croit lentement lorsque k' augmente (Cf. figure 6-8).
Figure
6-8 Variation du temps d'analyse en
fonction de k'.
| Pratiquement,
faire
varier le facteur de rétention k'
revient à: 1-
En HPLC
changer la phase mobile de manière à faire
varier le
coefficient de partition K
des produits à séparer (car k'
=K/b
)
On
peut ainsi changer le solvant
pour que k'
soit dans
l'intervalle optimum 1-5. (utilisation des gradients de solvant)
2-
En CPG
et HPLC, changer la phase stationnaire de manière
à faire
varier le coefficient de
partition K
des produits
à séparer. (car k'
=K/b
)
3-
En CPG
et HPLC faire
varier la quantité de phase stationnaire (en CPG
augmenter
l'épaisseur du film e
dans une colonne capillaire)
4-
En CPG
, faire
varier le
diamètre
intérieur (d)
de
la colonne (car k'
=K/b
=
4Ke/d).
5-
en CPG,
faire varier la température (car ln(k')
= -
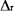 H/RT
+C) H/RT
+C) |
Solution.
| k' |
passe
de 2 à 5 |
passe
de 5 à 10 |
| R1/R2 | 1,25 |
1,36 |
| tr1/tr2 | 1,28 |
1,97 |
Ceci est un bon exemple des compromis auxquels on est confronté en chromatographie.
6-5-OPTIMISATION PAR LE NOMBRE DE PLATEAUX THÉORIQUES (N)
Figure 6-9 Influence de N sur la résolution |
Figure 6-10 Simulation de l'influence de N à 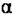 et k'constants
et k'constants |
D'après (equ.6-1), le temps d'analyse est proportionnel à N et à la longueur L de la colonne, il est multiplié par 2 si on double la longueur de la colonne.
Exercice d'application 6-5.
Pour améliorer une séparation, on décide de doubler la longueur de la colonne. Quel sera le résultat de cette décision sur R et tr ?
Solutions.| Pratiquement,
on peut augmenter
l'efficacité d'une colonne,
c'est à dire le nombre de plateaux théoriques N
en effectuant les manipulations
suivantes : 1-
En HPLC
diminuer la granulométrie du support de la phase
stationnaire.
2-
En CPG et HPLC,
augmenter la
longueur (L)
de la colonne
|
6-6-OPTIMISATION PAR LA VITESSE DE LA PHASE MOBILE (u)
|
figure
6-11 Courbe de Van Deemter
|
Étant donné l'équation de la courbe de Van Deemter : H = A +B/u + Cu (équ.2-8) La dérivé est égale à dH/du = -B/u2 + C cette dérivée est nulle pour uopt d'où uopt = √(B/C) et Hopt = A + 2√BC et Nopt = L/Hopt Cas particulier des colonnes capillaires : A= 0 d'où uopt = √(B/C) et Hopt = 2√BC donc Nopt =L/2 (√BC) En HPLC, on peut augmenter beaucoup plus qu'en CPG la vitesse de la phase mobile (u >uopt) sans trop de dommage pour la résolution. |
6-6-2 - Influence de la vitesse de la phase mobile sur le temps d'analyse
La formule (6-1) montre comment la vitesse de la phase mobile influe sur le temps d'analyse :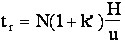
Exercice d'application 6-6
En CPG àk'(2-méthylpentane)
= 4 et k'(n-hexane)
=4,4
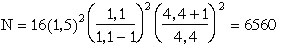
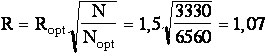
| Pratiquement,
on peut augmenter
l'efficacité d'une colonne,
en jouant sur le débit de la phase mobile en effectuant les
manipulations
suivantes: 1-
En CPG
et HPLC, changer la vitesse de la phase mobile (u)
pour atteindre uoptimal,
sur
la courbe de Van Deemter,
2-
En HPLC, Il faut toujours
avoir une
vitesse de phase mobile
supérieure ou égale à
uoptimal.
|
6-7- CONCLUSIONS SUR L'OPTIMISATION
Nous avons vu que les critères résolution, temps d'analyse et sensibilité sont interdépendants, toute modification de l'un d'entre eux a des répercussions sur les deux autres.| Paramètres
expérimentaux |
Résolution
(R)
x par : |
Temps
d'analyse (ta)
x par |
Quantité
maximum injectable (Qs)
x par : |
| Colonne Rayon intérieur (r) x2 Longueur (L) x2 |
¼ 1, 414 |
1 2 |
(>2) 2 |
| Phase
stationnaire épaisseur du film de phase stationnaire (e) x2 |
x(<1) |
2 |
2 |
| Phase
mobile (gaz vecteur) Débit optimal N2 Débit optimal N2 x3 Débit optimal He Débit optimal He x3 Débit optimal H2 Débit optimal H2 x3 |
1 ½ 1 ½ 1 ½ |
12 4 4,5 1,5 3 1 |
Inchangée |
| Température Température T T+ 30°C T+60°C de T à T+60°C (programmation de température) |
2,8 1,4 1,1 2,6 |
4 2 1 2 |
Inchangée |
6-8- PROBLÈMES SUR L'OPTIMISATION
Figure 6-11 |
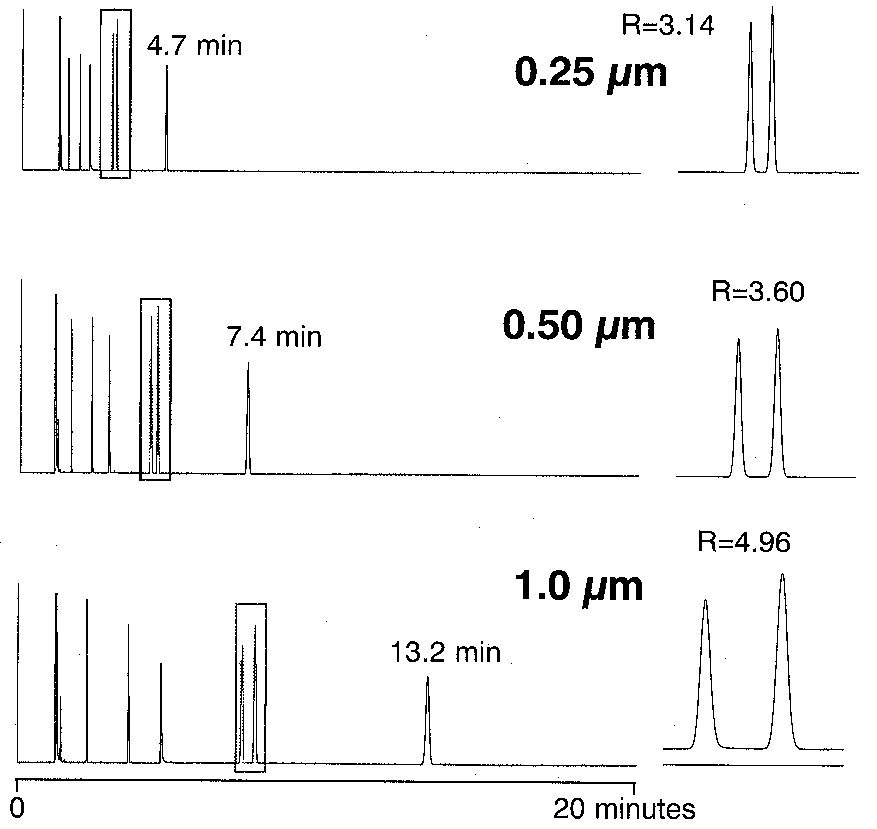 Figure
6-12
|
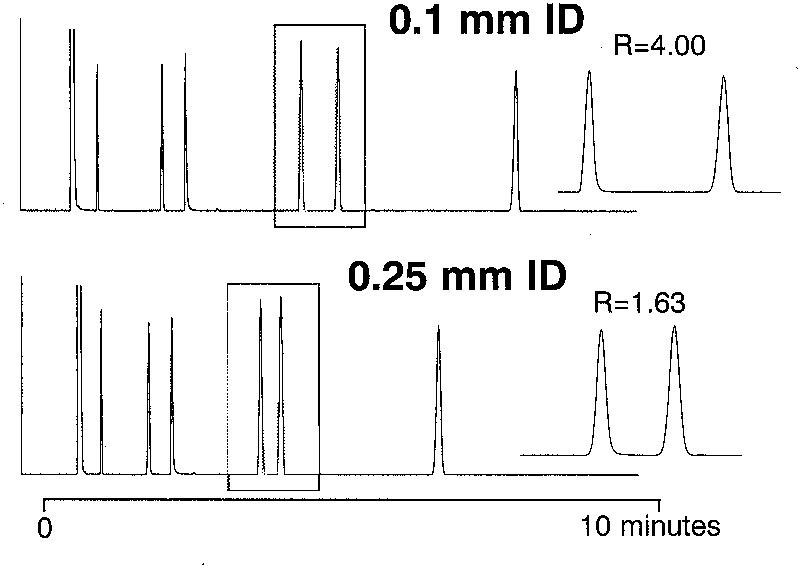 Figure 6-13 |
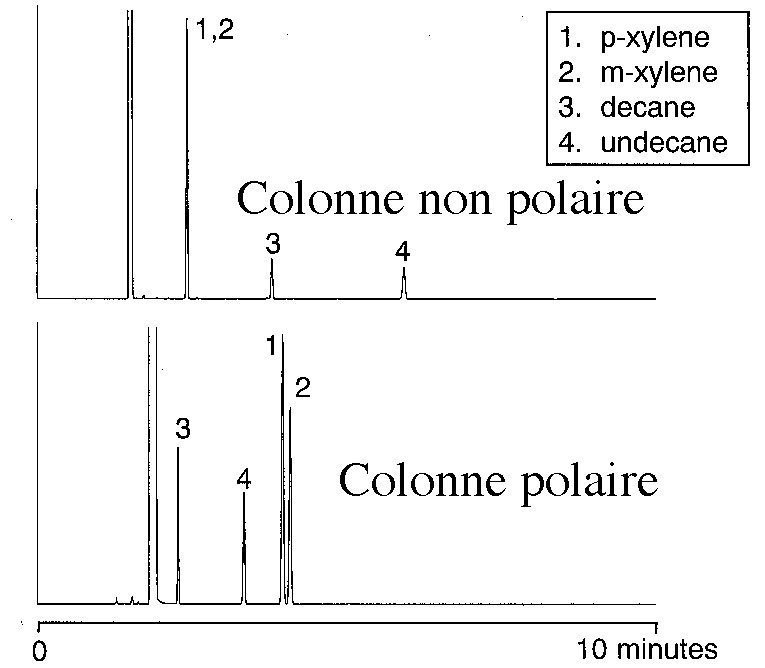 Figure 6-14 |
| L(m) |
15 |
30 |
60 |
| Tm
(mn) |
0,42 |
0,83 |
1,66 |
Théorique
Expérimental
R2/R1
1,414
1,419
R3/R2
1,414
1,426
ta2/ta1
2
2.02
ta3/ta2
2
2,04
| Colonne |
15
m |
30
m |
60
m |
| tr |
3,7 |
7.5 |
15,3 |
| k' |
7,8 |
8,03 |
8,18 |
Exercice
d'application
6-8.
|
Une
séparation 5 sucres a été obtenue en
HPLC analytique dans les conditions
suivantes : Conditions
Les
temps de rétention suivants ont été
mesurés :
Le
temps mort est 1,20 mn. Cette
séparation est-elle possible sur une
colonne HPLC préparative de 2500 plateaux
théoriques et
en maintenant une
résolution égale à 1 ? Les 2
colonnes ont des phases stationnaires
et mobiles identiques, une étude préliminaire a
montré que les facteurs de rétention sont
approximativement les mêmes pour les deux colonnes |
Solution
| n°
du pic |
1 |
2 |
3 |
4 |
5 |
| tr
(min) |
3,43 |
3,8 |
4,15 |
7,02 |
9,27 |
| k' |
1.86 |
2,167 |
2,46 |
4,85 |
6,725 |
| Doublet
de pics |
1/2 |
2/3 |
3/4 |
4/5 |
| facteur
de
séparation (a) |
1,165 |
1,134 |
1,97 |
1,39 |
|
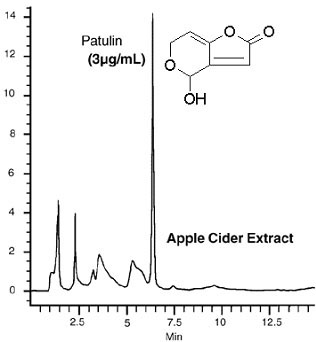
La patuline est une substance cancérigène qui se développe sur les pommes pourries, sa détection et son dosage sont obligatoires pour tous les produits finis à base pomme (jus, cidre…). Le
chromatogramme ci-contre démontre la
présence de patuline dans du cidre. Il a
été
obtenu sur une colonne analytique
A où NA
= On
décide d’isoler la patuline sur une
colonne préparative P avec NP
= Ces 2
colonnes ont des phases stationnaires
et mobiles identiques. De plus des tests préliminaires ont
montré que les
produits ont les mêmes facteurs de rétention sur
les 2
colonnes. Pourra
t’on isoler la patuline à l’aide la
colonne P ? |
 |
Solution: